|
|||||
|
|
| 基于PIV技术的压力场重构算法实现与研究 | |
| 引用本文: | 刘顺, 徐惊雷, 俞凯凯. 基于PIV技术的压力场重构算法实现与研究[J]. 实验流体力学, 2016, 30(4): 56-65. doi: 10.11729/syltlx20150119 |
| 作者姓名: | 刘顺 徐惊雷 俞凯凯 |
| 作者单位: | 南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室, 南京 210016 |
| 摘 要: | 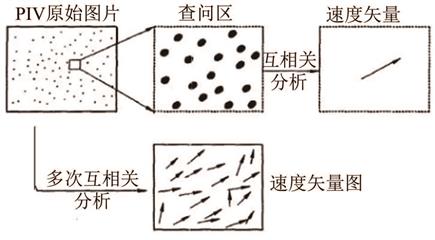 介绍了有限容积法、直接积分法和Poisson方程法3种基于PIV瞬时速度场重构压力场的基本原理以及相应的计算方法,选取管流突扩流场和偏置方块绕流流场两个不可压缩流场的瞬时速度场数据,采用上述3种压力场重构算法,分别研究了图像噪声、速度场精度、插值算法以及边界条件的类型与精度对重构压力场的影响。最后针对管流突扩过程第20ms的流场,给出了3种重构算法下的压力场云图以及对应的CFD模拟结果。 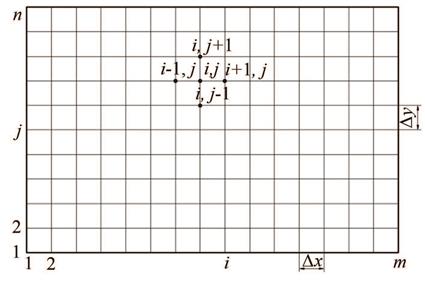 |
| 关 键 词: | PIV 速度场 重构压力场 Poisson方程 黎曼迭代 边界条件 |
| 收稿时间: | 2015-09-14 |
| 修稿时间: | 2015-12-17 |
| 点击此处可从《实验流体力学》浏览原始摘要信息 | |
| 点击此处可从《实验流体力学》下载免费的PDF全文 | |